【西川善司が語る”ゲームの仕組み” Vol.2】いつもの日常とゲームの世界では時間の流れ方が違う？ゲームは”離散時間”で出来ている

西川善司

ゲームの根本的な成り立ちについて重要なのは「ゲームと時間」の関係です。かつてゲームの伝説の人が言った「ゲームは1日1時間！」とは違います。さっそく、本題に入りましょう。

我々が住んでいる現実世界には時間が流れていますよね。もし、この時間が止まったらどうなるでしょうか。

そう、みんなピタっと止まって動かなくなるでしょう。そういう「時間が止まる」系の物語は漫画やアニメの世界では良く用いられるモチーフですが、実際、時間が止まった世界を見たことがある人はいません。

なぜなら現実世界では常に時間が流れていますし、仮に止まった瞬間があったとしても、我々にその事象を知覚することはできません。知覚にも時間が必要だからです。

それはそれとして、我々の現実世界の時間についてもう少し深く考えてみます。

時間は1分が60秒、1時間は60分…みたいな感じで捉えられていますよね。実生活で、よく用いられる時間の最小単位は1秒でしょうか。「そんな簡単なこと、”秒”で終わらせられるぜ」と強がったことのある人、いっぱいいると思います。

ただ、ストップウォッチを手に取って、徒競走のタイムを計測すれば、その表示画面上では1秒よりも小さい単位の数字が目まぐるしく動いていることに気がつきます。我々の時間は1秒よりも小さい単位で流れていることに気が付く瞬間です。

さて、薄型テレビの各画素は、電荷を与えることで指定の色に変化しますが、瞬間的に変わっているわけではありません。たとえば液晶画素の場合は、指定の色に変化が終わるまでに数ミリ秒掛かります。この時間を映像機器の世界では「液晶画素の応答速度」と呼んだりします。ちなみに1ミリ秒は1,000分の1秒で、1msと記載されます。最新のゲーミング液晶モニター製品の液晶画素の応答速度はまさに1msくらいです。

この応答速度、有機ELになるとマイクロ秒クラスになります。1マイクロ秒は1,000分の1ミリ秒、つまり100万分の1秒で、1μsと記載します。

これよりもっと微細な時間があります。

普段、プレイしているゲームを動かしているPC(コンピュータ)やゲーム機に搭載されているメモリー(DRAM)チップに対し、CPUやGPUが「データの読み出し」を指示して、実際に、CPUやGPUに読み出したデータがやってくるまでの待ち時間(レイテンシー)はどれくらいでしょうか。

メモリーの種類にもよりますが、だいたい15ナノ秒くらい掛かっています。1ナノ秒は1,000分の1μ秒、すなわち10億分の1秒で1nsと記載します。豆知識ですが、ゲーム機やコンピュータに用いられるメモリーのDDR1,DDR2,DDR3,DDR4,DDR5というメモリー種別は、DDRの数字が上がるほど世代が新しく、しかも伝送速度が上がっています。しかし、CPU/GPUからの読み出し指示から、最初のデータがやってくるまでのレイテンシーは初代のDDR1からほとんど変わっていないんです。

すみません。脱線しました。

では次。CPUやGPUにキャッシュメモリーが搭載されていますね。これらはSRAMというとても高速なメモリーなのですが、これのレイテンシーは数百ピコ秒です。1ピコ秒は1,000分の1ナノ秒。つまり1兆分の1秒で、1psと記載します。

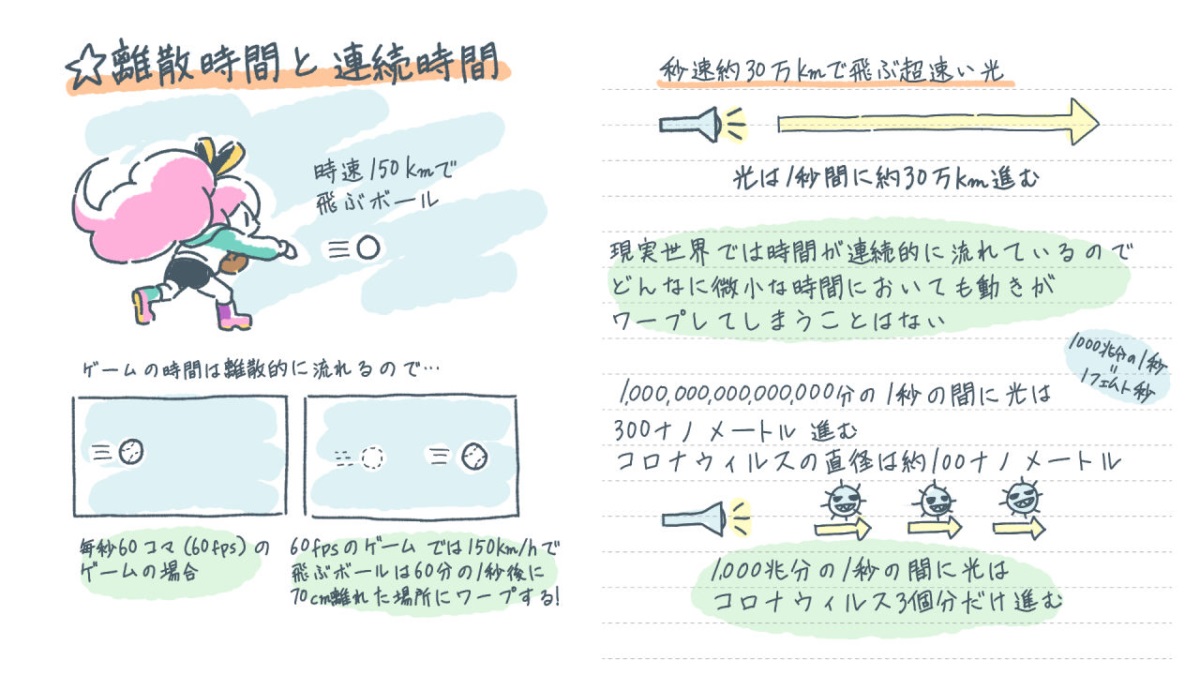
科学の世界ではさらに微細な1,000兆分の1秒のフェムト秒(fs)の話題が出てくることがあります。現実世界において最速である「秒速約30万km」の”光”ですら1フェムト秒(1fs)の間には300ナノメートルしか進みません。1ナノメートルは10億分の1メートルで1nmと記載します。

※フェムト(f)より小さい単位系としてはアト(a)、ゼプト(z)、ヨクト(y)が国際単位系として定義されている

そうそう、今、我々を苦しめているコロナウイルスは直径約100nmですから、光は1fsの間にコロナウイルス3つ分進むことが出来るわけですね。すみません、この連載ではこんな感じでたびたび脱線します。

だいぶ長くなりましたが、何が言いたかったかというと、我々の現実世界に流れている時間は、どんなに小さく分割してもキリがないということです。そして、その超々微細な短時間においても、何らかのモノが動いているということです。

やや強引な証明の仕方ですが、我々の現実世界の時間は結局のところ「連続」的に流れているということができそうです。一般に、我々の住む現実世界の時間は「連続時間」(Continuous Time)と呼んだりします。

時間の概念は、ゲームではどうなっているのでしょうか。

ゲームも、画面上のキャラクターの動きはスムーズですよね。サッカーのような球技系ゲームでは選手のキャラクターがフィールド上を縦横無尽に走り回りますし、選手が蹴ったボールはなめらかな弾道軌道を描いて飛翔し、そして地面に衝突すれば短い放物線を描いてバウンドもします。

「ゲーム世界」の時間の流れも、我々が住む現実世界と同じで「連続」時間なのでしょうか？実は、これは違います。ゲーム世界には、”飛び飛び”の「離散時間」(Discrete Time)が流れています。

連続時間と離散時間…なんだかかっこいいサイエンスな言葉の響きです。ただ、ちょっとピンときていない人も多いかもしれません。

次は、“離散”(Discrete)という概念についてもう少し理解を深めましょう。

我々が住む世界はアナログ的な概念に満ちあふれた世界ですよね。

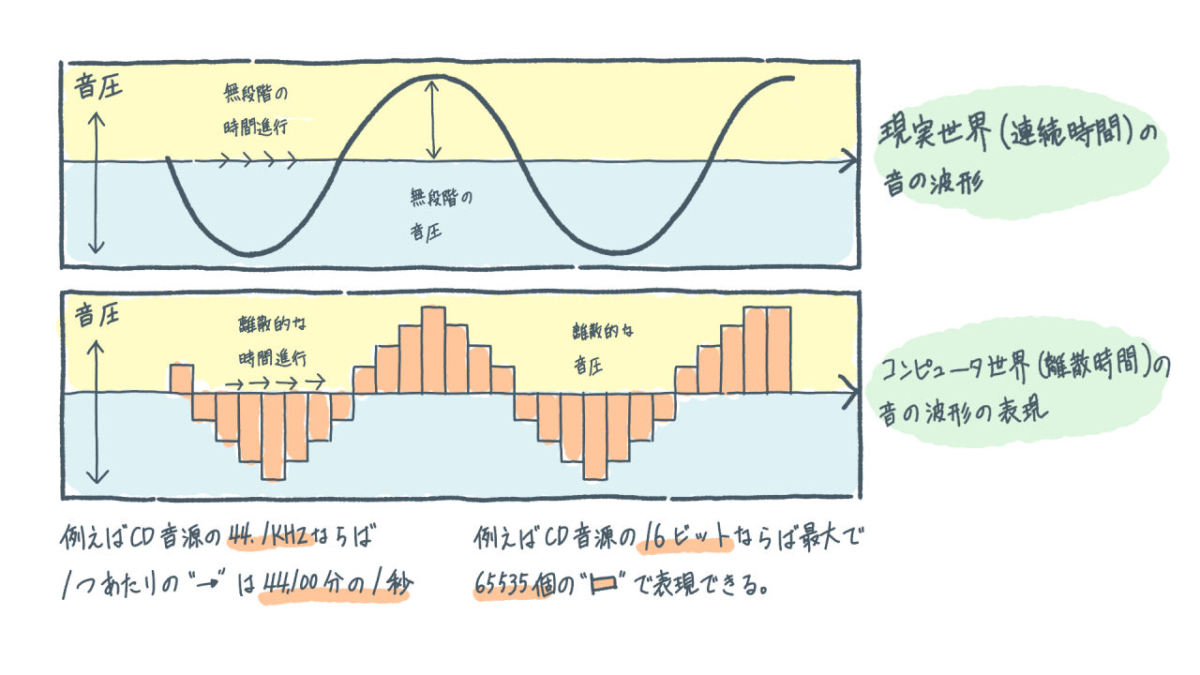
たとえば、耳で聞こえる「音」は、上下に細かく振れまくる折れ線グラフのような波形で出来ている「音波」だということを知っている人は多いでしょう。これを音楽CDではデジタル音波として数値化して記録しています。

音楽CDに記録されるデジタル音波は、音の強さ(音圧)を16ビット(0～65535)の範囲の数値で表現しています。

音楽もそうですし、音そのものが時間経過と共に進行して鳴るものですから、この数値化を時間経過とともに行う必要があります。音楽CDでは、この数値化を1秒間に44,100回の頻度で行ったデータを記録（標本化）しています。これが、音楽CDの仕様として有名な「サンプリングビット数16ビット、サンプリング周波数44.1kHz」に相当するモノです。

音楽CDは、なだらかな連続した曲線である現実世界のアナログ音波の波形を一定頻度で数値化したことで、連続性が欠落したカクカクのデジタル波形になりました。

このカクカクとした、あるいは飛び飛びの概念を「離散的」といいます。

デジタルは「0と1の世界」などと形容されることがよくありますが、デジタルは「離散的な概念」と言い換えることもできるかと思います。

コンピュータは、連続的なものを取り扱うよりも、離散的なものを取り扱うことが得意です。実際のところ、コンピュータの世界では連続的な概念を取り扱うことができないので(≒困難なので)、離散的な概念(≒デジタル的な概念)で扱うことで連続的な概念を近似して捉えることにしているという理解でもいいかもしれません。

そうそう、ゲームやコンピュータで取り扱う離散的なものとして分かりやすい物には、映像の解像度がありますよね。

我々の住む現実世界の情景には、1920×1080ピクセルのような固定的な数量で表される解像度の概念はないですよね。我々の肉眼を通して見た情景は、その眼球内の網膜に実装された視細胞の数や密度に依存した「解像度的な概念」は存在し得ますが、現実世界そのものの解像度は連続的、というかある意味では無限大といえます。

一方、ゲームで生成される情景は無限大の解像度で生成できませんから、GPUの性能に合わせて、1920×1080ピクセルのような離散的な解像度の映像として生成しているわけです。年々GPUの性能も向上していることもあり、最近のゲーム機では4K(3840×2160ピクセル)解像度を取り扱えるようになりましたが、これももちろん連続的なものではありません。

コンピュータは離散的な概念を取り扱うのが得意ということを理解してもらったところで、「ゲームの中で進行する時間」に話を戻すことにします。

コンピュータ上で動かすゲームは、やはり時間進行の概念を離散的に捉えています。離散時間は「デジタル時間」と言い換えてもいいでしょう。冒頭で、現実世界の時間進行を超微小なピコ秒まで見つめてきましたが、ゲーム内の時間進行はどこまで微小に分解できるのでしょうか。

それは大体、16.666…ミリ秒(ms)くらい…とおもってもらっていいと思います。

「見覚えのある数値だな」と気が付いた人もいるかもしれません。

そう、この「16.666…ms」(以下、16.67msと四捨五入して略記)は、60分の1秒のことです。

少しずつ分かってきましたね。ゲーム内の”離散”時間進行は、ゲーム映像の滑らかさの基準としてよく用いられる「フレームレート」(Frame Rate)と深く関係しているのです。

毎秒60コマ、すなわち60fps(Frames Per Second)で進行しているゲームは60分の1秒ペースの離散時間で進行しています。スムーズに動いて見えるゲームも(毎秒60コマのゲームの場合であれば)、実は16.67ms間隔の飛び飛びの離散時間で、ゲーム世界で起きている全ての出来事を計算して、次のゲーム世界の状態を更新しているのです。

連続するコマの中で、キャラクターの位置や物理シミュレーション、アニメーションが更新されている（実際、16.67ms単位でここまでの変化があるわけではないので、あくまでイメージとして受け取って欲しい）

サッカーゲームの例で行けば、フィールドを駆け回る選手キャラの手足の動きは16.67ms間隔で計算されます。選手キャラが蹴ったボールの軌道の計算、すなわち物理シミュレーションの演算も16.67ms間隔で行われます。非常に高速に動いている物体(オブジェクト)の物理シミュレーション演算は、たとえ60fpsのゲームであっても16.67ms間隔で計算していたのでは不都合が出てくる場合があります。

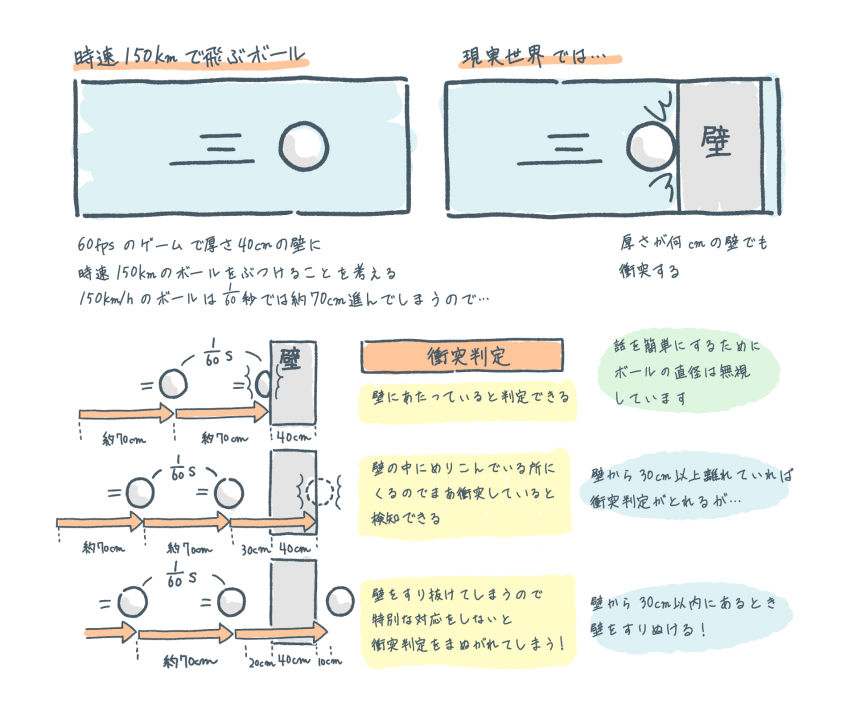
ここで、テニスや野球のような小さめのボールを取り扱うゲームを考えてみましょう。このボールを時速150kmで飛ばします。1時間に150km飛ぶボールは1秒間に41666.6mm(＝150,000,000mm÷3600秒)、大体42mくらい進みます。60fpsのゲーム、つまり、16.67msの間にこのボールが進む距離は約694.44mm(≒41666.6÷60)です。1フレームあたり約70cmくらい進むことになります。

たとえば、この時速150kmで飛んできたボールが、厚さ40cmの壁にボールが当たるか当たらないかの判定を行うとき、物理シミュレーションや衝突判定の実装の仕方によっては失敗することがあります。なんと、離散的な時間の概念で進むゲームでは、ボールが壁を突き抜けてしまうことがあり得るのです。

16.67msごとに約70cmも進んでしまうボールが、厚み40cmの壁に衝突できるのは、このボールが壁から約30cm～約70cm離れた位置にいるときだけです。この範囲内にいると、このボールは壁をすり抜けてしまいます。

この話を図解したものを下に示します。なお、話を単純化するために、下の図解ではボールの大きさを無視した点での衝突判定を行っています。

設計がやや甘めなゲームでは、こうした珍現象が実際に起こることがあります。こうした珍現象が起きてしまうのは、やはりゲーム世界が離散時間で処理されているからです。

では、このような珍現象が起きないようにするにはどうしたらよいのでしょうか。

直接的な対策は、この60fps、すなわち16.67ms間隔で進行している離散時間を縮めてやればいいことになります。

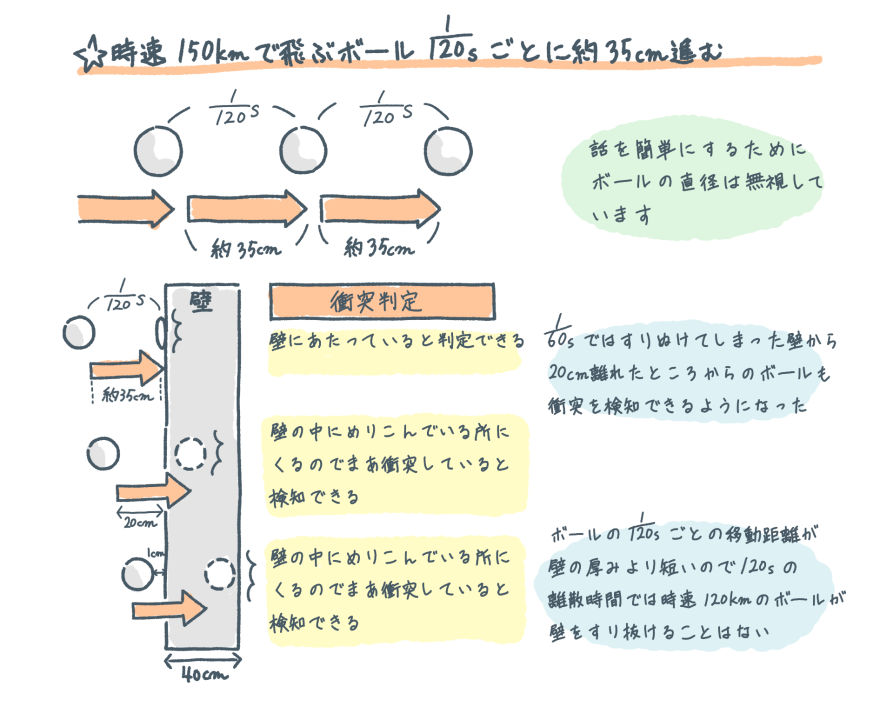
たとえば、前出の時速150kmのボールと厚み40cmの壁の衝突の事例で行けば、物理シミュレーションや衝突判定を120fps、8.33ms間隔で行えば、「壁のすり抜け」現象は免れそうです。というのも、時速150kmのボールは120fps、8.33ms間隔では約347.22mm(≒41666.6÷120)だけ進むことになり、この進行距離は、壁の厚み40cmよりも小さいので必ず、壁に衝突しますね。

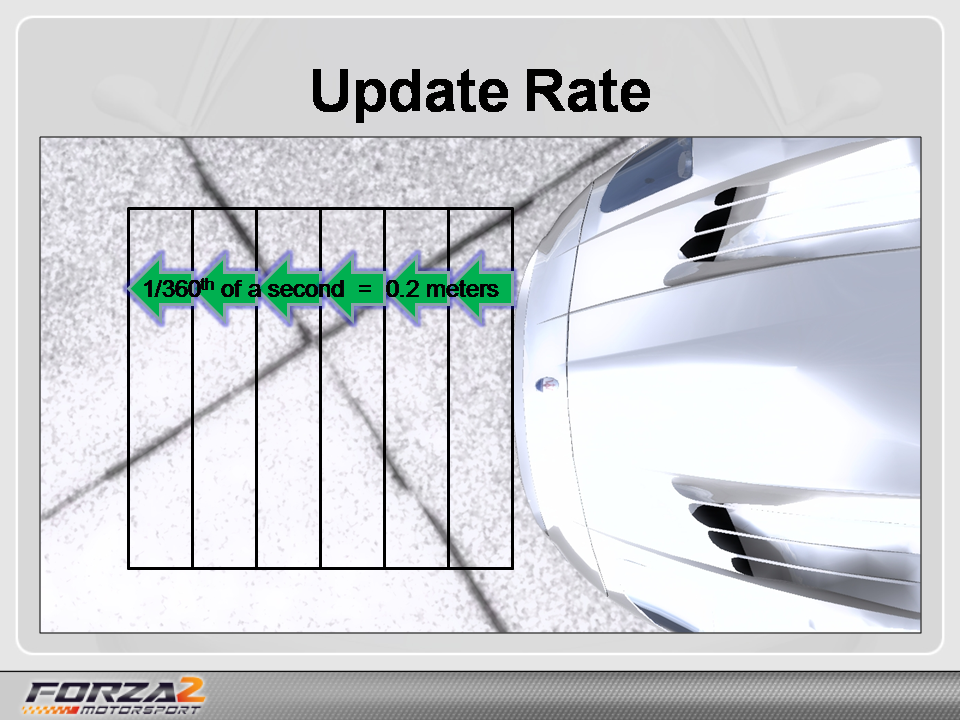
このように、とても速い動きを取り扱う一部のゲームでは、映像のフレームレートよりもより細かい微小時間間隔、たとえばフレームレートの2倍、3倍、4倍といった微小時間間隔で物理シミュレーションを行ったりすることがあります。実際にレーシングゲームなどでは、こうした実装になっている作品が存在します。

Xbox360向けのレーシングゲーム「FORZA MOTORSPORT2」ではゲーム映像のフレームレートは60fpsだが、車両物理シミュレーションは6倍の360fps相当の離散時間で行っていた

その理由は、時速300kmで走行しているスポーツカーの車両物理シミュレーションを60fps、16.67ms間隔で演算していたのでは1.3mおきになってしまう

360fps、2.8ms間隔で行えばこれを0.2m(20cm)単位の精度で計算できるようになる。当時、同作の開発チームは、高速走行状態の自動車の正確な姿勢演算を行うには、この離散時間精度が求められると判断した

ただ、いずれにせよ、ゲームが離散時間の進行で出来ている事には変わりはありません。そう考えると、現実世界って凄いですね。

今回は、ゲームにおける時間進行が離散時間で行われていることを解説してきました。

この事実が「ゲームのフレームレートと関係」に深く関わっていることも理解できたのではないかと思います。

最近では、ゲームを60fpsより高いフレームレートでプレイすることが、ゲームを競技的に楽しむeSportシーンなどを中心に広がってきていますよね。

しばしば「ゲームをそんなハイフレームレートでプレイする意味ってあるの？」と言われることがありますが、映像は60fpsで十分だとしても「ゲーム世界の物理現象を、現実世界の物理現象に近づけるためには必要なのかな…」と思えたりするかもしれません。

もっとも、上で例示してきたような「ゲーム物理の不具合」問題については、離散時間を60fps、16.67msのままで高精度な物理シミュレーションを行うアイディアも出てきています。たとえば、速度情報をあえて持たず、しかも離散時間精度にそれほど依存しない高品質な結果が得られる「位置ベースの物理シミュレーション」(Position Based Dynamics)という概念のゲーム物理がその一例です。このあたりの話題は専門的になるので、興味がある人は各自調べてみてください。

ところで、学校の物理の教科書に出てくる運動方程式の数々は、連続時間を基準にして書かれています。もし、今回取り上げた連続時間と離散時間の概念に興味を持ったのであれば、そうした運動方程式の数々を、60fps、16.67msの離散時間ではどういう風に考えればいいのか、ぜひ想像を巡らせてみてください。実際、これがゲームに物理シミュレーションを実装する際のアイディアの起点になってきます。

西川善司

プログラマーを経て技術系ジャーナリストへと転身。以降、半導体、ソフトウェア、グラフィックス、ディスプレイ、自動車、人工知能、ゲーム開発などの分野に注力した取材を行っている。